本文将对 Rank 类指标如 AUC-ROC,设计损失函数,从而实现直接优化。读到这我觉得就像当年学高数一样会有两类反应:这也要证?这也能证?如果你是第一种,那么文章的开头介绍了背景知识,看完你会变成第二种反应的。如果你是第二种,说明你对这个问题已经有了一些研究,那么可以直接从第三部分阅读。本文主要参考 Eban et al. (2016)。
Background
对于分类问题,为了度量一个模型的性能,我们构造出了很多指标,比如准确率、查全率(recall,有些地方翻译为召回率,我觉得还是查全率更直观一些)、\(F_{\beta}\)、ROC曲线等等,根据应用场景的不同,我们使用不同指标进行衡量,比如疾病筛选的时候我们认为把病人诊断为健康人的代价要远远大于把健康人诊断为病人,我们会更加强调查全率,或者我们希望使用\(P@R\),在规定查全率下尽量提高准确率。同时为了比较不同的模型,标量我们可以直接进行数值比较,为了处理如ROC曲线之类的指标,我们又构造了如平衡点(Break-Even Point)、AUC(Area Under Curve)等指标。
当我们根据场景选定指标后,就会将指标转化为损失函数,通过对损失函数的优化来达到指标的最大化。比如我们希望对准确率进行优化,实际上我们希望最小化
$$\frac{1}{m}\sum_{i=1}^{m} \mathbb I (f(x_i) \neq y_i)$$
其中 \(m\) 是样本个数,\(x_i, y_i\) 分别是第 \(i\) 个样本和其真实标记,\(f\) 是我们的学习器。通常我们希望我们的损失函数是可微的,从而可以很方便的使用 BP 算法对整个学习器的参数进行梯度下降。所以这时候我们做一些近似,使用 Cross Entropy 等替代示性函数,这样我们就将实际应用场景的要求转化为对一个可微函数的梯度下降求最优解的数学问题。随着数据的增加,我们的训练集动辄几十万上百万数据,没有办法一次性计算出损失再进行下降,但是从上式可以看出,不同样本之间的损失计算并没有依赖关系, 所以我们使用 mini-batch 的方式,每次使用一部分数据进行梯度下降,我们通过局部最小,来期望达到累加的和最小,从而实现海量数据分批的梯度下降。将批大小设置在 GPU 的处理宽度内,通过GPU最擅长的矩阵运算,大大加快了模型的收敛速度。这也是机器学习最基本的套路。
当然,事情远没有那么简单。我们以 AUC-ROC 为例来看一下 AUC 类的指标。关于 AUC 的详细介绍可以参考 周志华. (2016). 网上也有很多资料,这个比较基础,我就不介绍了。我们假定任意两个样本的预测值都不相同,那么 ROC 之上的面积可以表示为
$$1 – AUC = l_{rank} = \frac{1}{m^+m^-}\sum_{x^+\in D^+} \sum_{x^-\in D^-}( \mathbb I (f(x^+) < f(x^-))) $$
其中,\(x^+, m^+, D^+\) 分别代表正样本、正样本个数和正样本集合。我们希望这个函数最小。 即考虑每一对正反例,若正例的预测值小于反例则记一个罚分。若一个正例在 ROC 曲线上对应的坐标点是 \((x,y)\),那么 \(x\) 恰是排序其之前的反例所占的比例。AUC 实际上是随机选取一个正例和一个反例,正例的预测值高于反例的概率。
那么问题来了,这个损失函数既不可微,而且跟所有样本的排序有关(所以我们叫 Rank 类指标),也就是讲他既不能使用BP算法进行梯度下降,也不能像准确率一样分成小批,因为每个样本的损失不是孤立的,而是需要全局的排序才能计算。这一类的指标我们称之为 Non-Decomposable Measure。那么如何进行优化呢?尤其是对海量数据进行优化呢?这似乎是一个 Mission Impossible。
现行的做法是什么呢?我称之为随缘优化。
业界普遍的做法是对准确率这一类 Decomposable 的指标进行优化,以期待准确率上表现较好的学习器在 AUC 这类指标上也表现较好。翻遍所有的框架,包括 Keras、Pytorch、TensorFlow 等等,都只提供了一个 AUC 的度量指标,也就是对学习好的模型进行评测一下,并没有提供直接对 AUC 优化的损失函数。实际上这种做法很随缘,我们假设训练集中有5个数据,三个正例两个反例,学习器1和学习器2对这个5个样本的打分分别为
$$S_1 = \{0.9, 0.8, 0.3, 0.7, 0.6\}\\ S_2 = \{0.8, 0.7. 0.6, 0.9, 0.3\}$$
以0.5为阈值,则学习器1的准确率为50%,学习器2为75%。但是很容易看出来,\(AUC_1 = \frac{2}{3}, AUC_2 = \frac{1}{2}\)



过去几十年,大家都是这么做的,并不直接对 AUC 类指标进行优化,默认准确率较高的分类器在AUC等指标上也表现较好,将精力集中在模型结构的创新上。当然也有一些工作,前期的工作主要集中在对函数的近似,也即示性函数近似成可微的函数,比如 Yan et al. (2003),但并没有解决数据之间的全局依赖,从而也就无法应对越来越多的大规模数据的divide and conquer,最近的一些工作如 Narasimhan, H., Kar, P., & Jain, P. (2015, June) 开始在一些特定模型,如广义线性模型上进行优化,下面我们介绍 Google 在最近发表的 Eban et al. (2016) 中的方法,通过分析损失函数的上下界,来对 AUC 构造出可微可分解的损失函数。
Preliminary
首先我们定义一个二分类学习器 \(f_b, f: X \to R, b \in R\),当\(f(x) \geq b\)时,样本被分类为正例。那么我们可以计算出真正例(tp, true-positive)和假正例(fp, false-positive)的个数 $$tp = \sum_{i \in Y^+} \mathbb I (f(x_i) \geq b)\\
fp = \sum_{i \in Y^-} \mathbb I (f(x_i) \geq b) $$
如果我们使用0-1损失函数,那么上式即
$$\begin{align} tp &= \sum_{i \in Y^+} 1 – l_{01}(f_b, x_i, y_i)\\
fp &= \sum_{i \in Y^-} l_{01}(f_b, x_i, y_i) \end{align}$$
如果使用hinge loss:\(l_h(f_b, x_i, y_i)\),那么很明显的\(l_h \geq l_{01}\)。所以我们定义 \(tp\) 的下界 \(tp_l\) 和 \(fp\) 的上界 \(fp^u\):
$$ \begin{align} tp_l &= \sum_{i \in Y^+} 1 – l_h(f_b, x_i, y_i) \leq tp\\
fp^u &= \sum_{i \in Y^-} l_h(f_b, x_i, y_i) \geq fp \end{align} $$
使用 log loss、smooth hinge loss 等其他的函数去构造 0-1 loss 的上界原理相同,都将 \(tp_l, fp^u\) 化为了凸函数,后面我们将利用他们的凸性,将AUC等指标转化为凸优化问题。
Maximize R@P
下面我们先对 \(R@P\) 进行优化,即在保证准确率的情况下最大化查全率。即:
$$R@P_{\alpha} = \max R(f) \quad s.t. \quad P(f) \geq \alpha$$
同时,我们看到
$$\begin{align} P &= \frac{tp}{tp+fp} \\
R &= \frac{tp}{tp + fn} = \frac{tp}{|Y^+|}
\end{align}$$
所以原优化问题变为:
$$\max \frac{1}{|Y^+|} tp \quad s.t. \quad tp \geq \alpha(tp + fp)$$
使用上面我们得到的上界和下界对优化问题进行缩放,我们得到缩放后的问题:
$$\overline{R@P_{\alpha}} = \max \frac{1}{|Y^+|}tp_l \quad s.t. \quad (1 – \alpha)tp_l \geq \alpha fp^u$$
不难看出,我们可以通过对 \(\overline{R@P_{\alpha}} \) 优化,来实现原问题的优化。
我们定义在所有正例上的loss:
$$\mathcal{L}^+ = \sum_{i \in Y^+} l_h(f, x_i, y_i)$$
同理定义\(\cal L^-\),并将 \(tp_l, fp^u\) 显式代入,我们得到:
$$ \overline{R@P_{\alpha}} = \max 1 – \frac{\mathcal{L}^+}{|Y^+|} \\ s.t. \quad (1 – \alpha)(|Y^+| – \mathcal{L}^+) \geq \alpha \mathcal{L}^- $$
忽略一些常数项,变形后得到:
$$\begin{align}&\min \mathcal{L}^+\\
&s.t. \alpha \mathcal{L}^- + (1 – \alpha)(\mathcal{L}^+ – |Y^+|)\end{align}$$
使用推广的拉格朗日乘数法,我们得到:
$$\min_{f} \max_{\lambda \geq 0} \mathcal{L}^+ + \lambda[ \alpha \mathcal{L}^- + (1 – \alpha)(\mathcal{L}^+ – |Y^+|) ]$$
整理后有:
$$ \min_{f} \max_{\lambda \geq 0} [1 + \lambda(1 – \alpha)]\mathcal{L}^+ + \lambda \alpha \mathcal{L}^- – \lambda(1 – \alpha)|Y^+|$$
这时候我们就可以分别对 \(f, \lambda\) 进行梯度下降和“梯度上升”进行优化。而当 \(\cal L^+, L^-\) 为凸函数时,Nedić, A., & Ozdaglar, A. (2009) 证明了这个过程会收敛到一个固定点。上式也可以看做分别对正例和反例添加了\( [1 + \lambda(1 – \alpha)]\),\(\lambda \alpha \) 两个权重,不同的是 \(\lambda\) 在一直进行梯度上升。
Here We Go
有了上面的基础,下面我们分析AUCPR。AUCPR实际上就是在 \(\alpha\) 上对\(R@P_{\alpha}\) 进行积分,即:
$$AUCPR = \max_f \int R@P_{\alpha} d\alpha$$
自然而然的我们想到使用分段求和进行近似,那么我们有:
$$ \min_{f,b_1,\dots, b_k} \max_{\lambda_1,\dots, \lambda_k \geq 0}\sum_{t=1}^k \Delta_t [1 + \lambda_t(1 – \alpha_t)]\mathcal{L}^+(f, b_t) + \lambda_t \alpha_t \mathcal{L}^-(f, b_t) – \lambda_t(1 – \alpha_t)|Y^+|$$
上式同样可以使用 (min-batch) SGD 进行优化,从而我们完成了Mission Impossible。将被积函数替换成true positive rate at fixed false positive rate,那么就可以实现文章前面我们所讲到的AUCROC。
Performance
作者对这个算法的性能进行了测试,并对比了传统的对准确率进行优化的loss函数,测试结果就特别好,然后收敛很快,这里我贴下图,就不详细解释了,可以阅读原文。
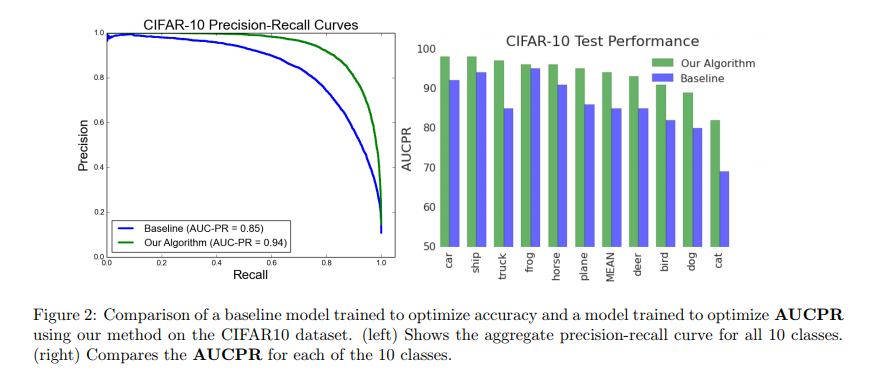
What’s More
之所以不对结果再详细解释,还有一个原因就是我在kaggle的一个任务上使用上述算法,性能非但没有提升,而是有显著下降。所以文章虽然提出了一个很好的算法,但是在性能的测试上是否有 data snooping?算法的稳定性或者适用条件(比如准确率已经高达95%以上是否还能通过这种优化达到一个提升)我认为是后续的一个研究方向。
Pytext 和 Tensorflow Research 中实现了文中的算法。源码的注释非常完善,我这里就不做解读了,可以直接点开链接阅读。值得注意的是,TensorFlow Research 中对AUCROC的实现并非是按照原文的思路进行的,而是将AUCROC视为我们前面所讲的正确排序的概率,在每个 batch 中使得这个概率最大,以期达到全局最优。
另外,Sanyal et al. (2018) 是非常不错的延伸阅读材料。利用对偶理论提出了新的算法。
Some Thoughts
最后插些题外话,上个月参加了在南京举办的全球人工智能大会,我特别去听了下人工智能金融科技的分论坛,包括平安集团的技术负责人等很多业界大佬都参与了分享,目前人工智能在金融领域的发展更多的是应用场景的拓展,对人工的替代,对效率的提升,比如智能客服、保险欺诈预警等等。当然这些都是很棒的应用,但我觉得多少是令量化交易者有些失望,我们并没有看到人工智能选股、人工智能交易,诸如此类,是大家对此都秘而不宣吗?
在我看来,机器学习只是用计算机模型的形式降低了统计科学的应用门槛,使其更加便利地应用于各个行业,但是在数学或者所在的行业没有突破的前提下,不能指望机器学习成为解决所有问题的银弹。尤其对于量化的研究人员要更加警惕,看着机器学习在NLP、CV领域不断大放异彩,难免会产生错觉,就像和有钱人一起相处久了,总觉得自己也是有钱人了。人本身在语言处理和图像识别上就是专家,或者说人类证明了这些东西是有模式可循,机器朝着 Human-Baseline 去努力,而对量化交易而言,我们甚至不知道Human-Baseline在哪,我想这就是为什么很多人对于机器学习直接应用于量化交易而感到迷茫的原因吧。我也推荐一下之前很火的一篇文章,张钹院士关于人工智能的一个访谈。
令人矛盾的是,对比宏观的时间跨度,在高频尺度下,数据的模式往往更加清晰,相对于使用高深的数学硬刚,我们或许可以通过机器学习训练出更加准确的模型来预测未来的方向,但这些优势又可能被笨重的模型带来的延时所拖累。如果能将模型的黑盒打开,精简出模型的精髓,那么一定会为高频交易交易翻开新的篇章,遗憾的是,这也是机器学习所面临的最大的瓶颈,倘若能打开黑盒,高频交易、机器学习乃至整个人类的科学认知都将进入一个完全不同的维度,这可能才是真的 Mission Impossible。
Reference:
Eban, E. E., Schain, M., Mackey, A., Gordon, A., Saurous, R. A., & Elidan, G. (2016). Scalable learning of non-decomposable objectives. arXiv preprint arXiv:1608.04802.
Narasimhan, H., Kar, P., & Jain, P. (2015, June). Optimizing non-decomposable performance measures: A tale of two classes. In International Conference on Machine Learning (pp. 199-208).
Nedić, A., & Ozdaglar, A. (2009). Subgradient methods for saddle-point problems. Journal of optimization theory and applications, 142(1), 205-228.
Sanyal, A., Kumar, P., Kar, P., Chawla, S., & Sebastiani, F. (2018). Optimizing non-decomposable measures with deep networks. Machine Learning, 107(8-10), 1597-1620.
Yan, L., Dodier, R. H., Mozer, M., & Wolniewicz, R. H. (2003). Optimizing classifier performance via an approximation to the Wilcoxon-Mann-Whitney statistic. In Proceedings of the 20th International Conference on Machine Learning (ICML-03) (pp. 848-855).
周志华. (2016). 机器学习. 清华大学出版社.
